[ML] 회귀 모델평가지표, 변수 스케일링 이해하기

학습 키워드 : 랜덤포레스트, 평가지표, 회귀, Logarithm, 이상치, 희소값, 이산화

---

✔️ 키워드

• 랜덤포레스트 회귀(RandomForestRegressor)
• 회귀 모델평가지표(MAE, MSE, RMSE, RMSLE)
• 로그(Logarithm)
• 이상치(outlier), 희소값
• 변수 스케일링(Feature Scaling)
• 이산화, cut, qcut

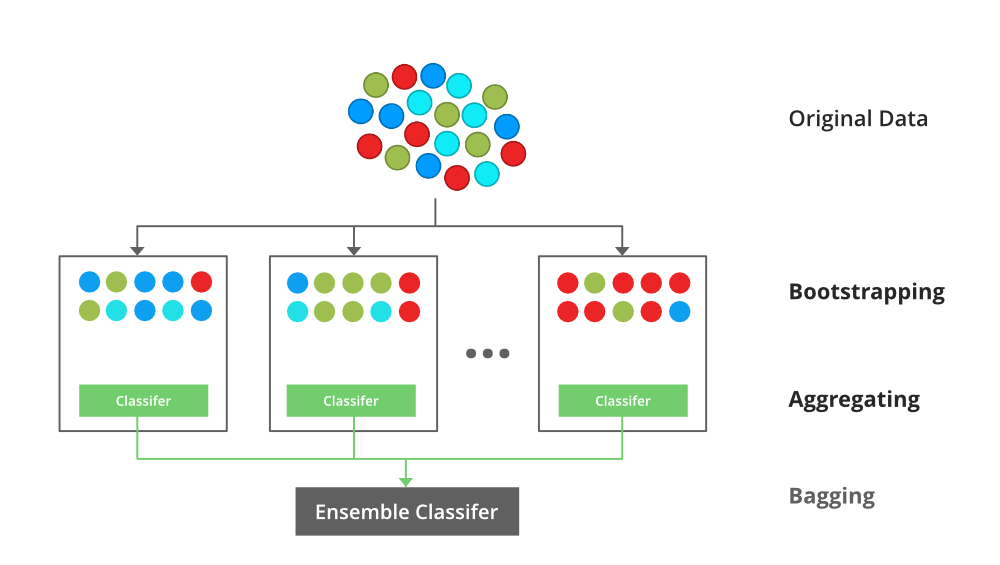
✔️ 랜덤포레스트

랜덤 포레스트는 앙상블 기법 중 하나이다.
여러 개의 의사결정나무를 만들고, 그들의 다수결로 결과를 결정하는 방법

Fig 1. 부트스트랩 집계(배깅) 개념에 대한 그림

✔️ 회귀 모델 평가지표

회귀의 평가를 위한 지표는 실제 값과 회귀 예측값의 차이를 기반으로 한다.
오차값이 작을수록 회귀 성능이 좋은 것입니다.
예측값과 실제값의 차이가 없다는 뜻 때문임

(1) MAE(Mean Absolute Error)

• 모델의 예측 값과 실제 값 차이의 절대 값에 대한 평균값
• 절대 값을 취하기 때문에 가장 직관적임

MAE 지표 계산식

(2) MSE(Mean Squared Error)

• 모델의 예측 값과 실제 값 차이의 면적(제곱)의 합
• 제곱을 하기 때문에 특이치에 민감
• 정답에 비해 예측값이 매우 다른 경우, 그 차이는 오차값에 상대적으로 크게 반영

MSE 지표 계산식

🔍 MAE와 MSE 비교

• 차이점 : MSE는 제곱을 해주고 MAE는 제곱은 하지 않고 절대값을 구함
• 공통점 : 실제값과 측정값을 빼주는 것, 평균을 내는 것
• 🤔 비슷한 것 같은데, 데이터 분석에서 둘의 사용법이 다른 이유
  • 평균제곱오차(MSE)는 회귀에서 자주 사용되는 손실함수
  • 일반적인 회귀 지표는 평균절대오차(MAE)
  • 즉, MSE는 손실함수로 쓰이고 MAE는 회귀지표로 사용됨

(3) RMSE(Root Mean Squared Error)

• MSE에 루트를 씌운 값
• 지표를 실제 값과 유사한 단위로 다시 변환하기에 MSE보다 해석이 쉬움
• MSE보다 이상치에 Robust 하다
• 오차가 클수록 가중치를 줌(오차 제곱의 효과)

RMSE 지표 계산식

(4) RMSLE(Root Mean Squared Log Error)

• RMSE에 로그를 취한 값
• 오차가 작을수록 가중치를 줌(로그의 효과)
• 주로 최솟값과 최댓값 차이가 큰 경우에 사용됨
  • 예 : 부동산 가격

RMSLE 지표 계산식

🔍 RMSE와 비교했을 때 RMSLE의 장점

• 아웃라이어에 robust(강건)하다
• 상대적 Error 를 측정해 줌
  • 예측값과 실제값에 로그를 취해주면 로그 공식에 의해 상대적 비율 구할 수 있음
• Under Estimation에 큰 패널티 부여
  • 예측값이 실제값보다 클 때보다 예측값이 실제보다 작을 때 더 큰 패널티 부여

✔️ 로그(Logarithm)

정규분포 형태를 만들어주기 위해 Log Transformation이 필요하다.
log 함수가 x값에 대해 상대적으로 작은 스케일에서는 키우고, 큰 스케일에서는 줄여주는 효과가 있기 때문이다.

데이터에 따라 치우치고(skewed) 뾰족한 분포가 정규분포에 가까워지기도 한다.
log를 취한 값을 사용하면 이상치에도 덜 민감하다.

Fig 2. 일반적으로 사용되는 세 가지 밑이 있는 로그 함수 플롯

(1) 로그 함수의 특징

로그 함수의 특징은 다음과 같습니다.

• 밑이 더 작은 값에 기울기가 가파르고 값이 커질수록 기울기가 완만해짐
  • 밑이 작은 로그 함수는 밑이 큰 로그 함수보다 x 값들에 대해서 y 값의 차이가 큼
• 0 < x < 1 범위에서는 기울기가 매우 가파름
  • x 가 (0, 1) 사이의 값을 가지면 y는 (0, -∞) 사이의 값을 가짐
• x 값이 점점 커짐에 따라 로그함수의 기울기는 급격히 작아짐
  • x 에 큰 값이 들어가도 y 값이 크게 차이나지 않음
  • 즉, 넓은 범위를 가지는 x를 비교적 작은 y 값 구간 내에 모이게 함

(2) 로그 변환(Log Transformation)

데이터 분석에서 로그를 취하는 이유는 정규성을 높이고 분석에서 정확한 값을 얻기 위함이다.
데이터 간 편차를 줄여 왜도(skewness)와 첨도(Kurtosis)를 줄일 수 있기 때문에 정규성을 높일 수 있다.

Fig 3. 로그변환 전(왼쪽), 후(오른쪽) 그래프

🚨 주의 사항

머신러닝 모델을 만들 때, 정답값(label)에 로그 변환해주었다면 아래 주의 사항을 기억하자.
모델 학습과정에서 log 적용했다면, 답안 제출 시 exp를 적용하여 원래 형태로 복원한 후 제출해야 한다.
log에 음수가 들어가면 nan 값으로 반환된다는 점을 고려하여 log 함수 사용 시 최솟값을 더해 음수가 입력되지 않도록 주의해야 한다.

import numpy as np

# 넘파이에서 제공하는 log 기능 
# np.log1p(x)와 np.log(x+1) 는 같은 기능을 한다
np.log1p(x) == np.log(x + 1)

# 넘파이에서 제공하는 exp 기능
# np.expm1(x)와 np.exp(x)-1 는 같은 기능을 한다.
np.expm1(x) == np.exp(x)-1

✔️ 이상치(Outlier)

수치형 변수(Numerical Feature)에서 대부분 값이 갖는 범위를 벗어난 값을 의미한다.
이상치가 있다면 머신러닝 모델이 과대적합/과소적합 될 수 있으며 결과값의 정확도를 낮춘다.

(1) 이상치 발생 이유

• 데이터 수집 과정
• 데이터 조작 과정
• 예외적으로 수치 뛰어오른 경우

(2) 이상치 찾는 방법

• 일정 범위에서 동떨어져 있는 경우
• 시각화 또는 기술통계
• 박스플롯(boxplot)에서 범위 벗어나는 경우
• 도메인 지식에 근거해서 정할 수 있음

✔️ 희소값

범주형 변수(Categorical Feature)에서 빈도가 낮은 값을 의미한다.
희소값을 병합(combine)하고 One-Hot-Encoding 하면 변수의 개수를 줄일 수 있다.

(1) 희소값 발생 이유

• 데이터 수집 과정에서 자연스럽게 비율 높은 것과 낮은 것이 생김
• 비율이 낮은 것이 희소값이 됨

(2) 희소값 찾아야 하는 이유

• 데이터 해석을 어렵게 하고 머신러닝 성능을 낮출 수 있음
• 데이터 경향을 파악하기 어려움

# 희소값 찾는 방법 1 
# 데이터의 개수가 많은 값부터 내림차순으로 정렬
df[컬럼명].value_counts()
# 데이터의 개수가 적은 값부터 보고 싶다면 다음과 같은 코드를 작성하면 됨
df[컬럼명].value_counts(ascending=True)

# 희소값 찾는 방법 2
n = df[컬럼명].value_counts()
sns.countplot(data=df, x="컬럼명", order=n.index);

✔️ 변수 스케일링(Feature Scaling)

Feature의 범위를 조정하여 정규화하는 것을 의미한다.
일반적으로 Featurea의 분산과 표준편차를 조정하여 정규분표 형태를 띄게 하는 것을 목표로 한다.

Fig 4. 4가지의 확률 밀도 함수, 붉은 색은 표준정규분포

(1) 변수 스케일링 필요성

• Feature의 범위가 다르면 변수간의 비교가 어려움
• 일부 머신러닝 모델에서는 제대로 작동하지 않음
• 트리 알고리즘에서는 절대적인 값보다 상대적인 값에 영향을 받기 때문에 스케일링에 영향이 크지 않지만, 다른 알고리즘에서는 스케일링 값을 조정해 주면 모델의 성능이 좋아짐

(2) 변수 스케일링 기법

이름	정의	공식
Normalization - Standardization (Z-score scaling)	평균을 제거하고 데이터를 단위 분산에 맞게 조정	z = (X - X.mean) / std
Min-Max scaling	변수를 지정한 범위로 확장하여 기능 변환(기본값:[0, 1])	X_scaled = (X - X.min) / (X.max - X.min)
Robust scaling	중앙값 제거하고 분위수 범위(기본값 IQR)에 따라 데이터 크기 조정	X_scaled = (X - X.median) / IQR

🔍 변수 스케일링 기법의 장단점

• 표준화(Z-score) : 평균을 빼주고 표준편차로 나눔
  • 장점 : 표준편차가 1이고 0을 중심으로 하는 표준 정규 분포를 갖도록 조정
    • 평균 0, 표준편차 1의 특징을 가짐
  • 단점 : 평균을 이용하여 계산하기 때문에 이상치에 영향을 받음
• Min-Max : 0 ~ 1 사이값으로 만듦
  • 변수 범위를 0과 1 사이의 값으로 압축해줌
  • 단점 : 이상치를 포함하고 있으면 범위 설정에 영향이 가기 때문에 이상치 영향을 받음
• Robust : 중간값을 빼주고 IQR값으로 나눔
  • 중앙값과 사분위 수를 이용한 스케일링 기법
  • 편향된 변수에 대해 변환 후 변수의 분산을 더 잘 보존하기 때문에 이상치 제거에 효과적
  • 장점 : 표준화 기법과는 다르게 중앙값을 이용하기 때문에 이상치의 영향을 덜 받음

# 사이킷런에서 제공하는 Feature Scaling의 종류 
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import RobustScaler

(3) 알아둘 점

• 스케일링 전, 후 countplot에서 보면 분포의 형태는 변함이 없다.
• 하지만, 변수의 범위가 달라졌고 이는 기술통계값(describe)으로 명확하게 확인할 수 있다.

✔️ 이산화

수치형 변수(Numerical Feature)를 일정 기준을 나누어 그룹화 하는 것을 의미한다.
예 : 연령을 10대, 20대, 30대 식으로 10살을 단위로 나눠 분석하면 경향이 뚜렷해지고 이해하기 쉬워진다.

(1) 이산화 필요성

• 머신러닝 알고리즘에 힌트를 줄 수 있음
• 머신러닝이 너무 세분화된 조건으로 오버피팅(과대적합)되지 않도록 도움을 줄 수 있음
• 유사한 예측강도를 가진 유사한 속성을 그룹화하여 모델 성능 개선에 도움을 줄 수 있음

(2) 이산화 방법

이산화는 pandas에서 제공하는 pd.cut() 과 pd.qcut()으로 그룹을 나눌 수 있다.
pd.cut() : 비슷한 길이로 나누는 것 (고객을 구매 금액 구간에 따라 등급 나눌 때)
pd.qcut() : 비슷한 비율로 나누는 것 (고객을 나눌 때 고객의 수를 기준으로 등급 나눌 때)
👉 pd.cut, pd.qcut 함수 정의 및 파라미터 보러가기

Fig 5. pd.cut()과 pd.qcut() 비교

✔️ Reference

• 🦁 박조은 강사님 강의 자료 :)
• 📷 Fig 1 출처 : Bagging vs Boosting in Machine Learning
• 📷 Fig 2 출처 : 위키백과, 우리 모두의 백과사전 - Logarithm
• 📷 Fig 3 출처 및 로그 부분 정리 - 내 블로그
• 티스토리 by 흰곰곰 - Random Forest Regression ( 랜덤포래스트 회귀 ) 개념 및 python 예제
• 티스토리 by JG Ahn - RMSLE (Root Mean Squared Log Error)
• 티스토리 by 우노 - [ML] 데이터 스케일링 (Data Scaling) 이란?
• 티스토리 by Haeon - 데이터 스케일링 (Data Scaling)
• Medium by Jone - 피처 스케일링 시작하기
• 티스토리 by 뭉지(moonz) - 데이터 전처리 (2. 피처 스케일링)
• stack overflow - Difference between standardscaler and Normalizer in sklearn.preprocessing
• Medium by Sharoon Saxena - What’s the Difference Between RMSE and RMSLE?

개인 공부 기록용 블로그입니다
오류나 틀린 부분이 있을 경우 댓글 혹은 메일로 따끔하게 지적해주시면 감사하겠습니다 :)