[TIL] 표본분산에서 n이 아닌 n-1로 나누는 이유
모분산과 표본분산
모집단은 실험 대상의 전체 집단을 말하며 모집단(관심의 대상이 되는 집단)의 특성을 측정하는 전수조사는 사실상 어렵다. 이러한 이유로 많은 수의 표본을 무작위로 뽑아 정의된 식을 통해 모평균이나 모분산과 같은 모분포의 특성을 추정한다. 이때 표본이 무작위로 뽑힌다는 점에서 그로부터 계산된 값 역시 무작위성을 가진다. 즉 모분산의 어떤 값을 추정하기 위해 표본들로부터 계산된 값은 확률변수가 된다.
다시 정리해 보면, 표본평균과 표본분산은 모집단의 모평균, 모분산을 추정하기 위해 고안된 추정량으로 그 자체는 확률변수이다. 특히 표본분산의 기대값이 모분산과 같다는 점에서 표본분산이 모분산의 불편 추정량이 된다.
cf. 불편 추정량이란 추정량의 기대값이 모수와 같아질 때의 추정량을 말한다.
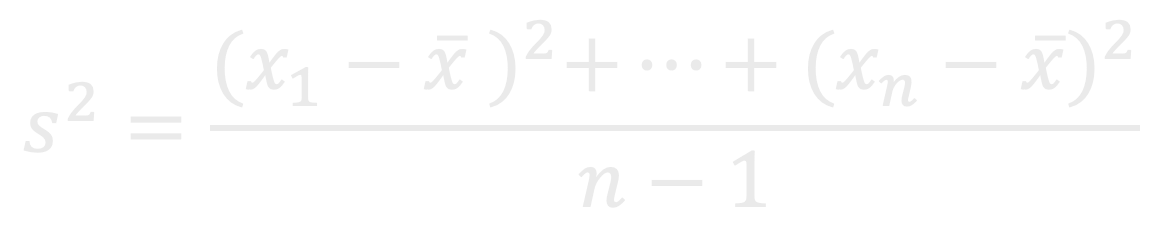
통계에서 표본분산을 구할 때 n이 아닌 n-1로 나누는데 그 이유는 n-1로 나누는 것이 값의 정확도가 더 높기 때문이다.
[표본들이 모평균에서 퍼진 정도] = [모분산] = [표본들이 표본평균에서 퍼진 정도] + [표본평균이 모평균에서 퍼진 정도]
모집단에서 무작위로 추출된 표본은 모집단보다는 데이터간의 편차가 작을 것이다(모집단에서 평균에 가까운 값이 확률적으로 추출될 가능성이 높기 때문). 퍼짐의 정도가 모집단보다 표본이 좁다. 따라서 표본분산으로 모분산을 추정할 때 최대한 근접하게 추정하기 위해선 분모를 작게 만들어 추정값을 더 커지게 보정할 필요가 있다.
보정을 위해 표본분산을 구할 때 n이 아닌 n-1로 나누게 되는데 이 보정을 베젤 보정(Bessel’s correction)이라고 한다.
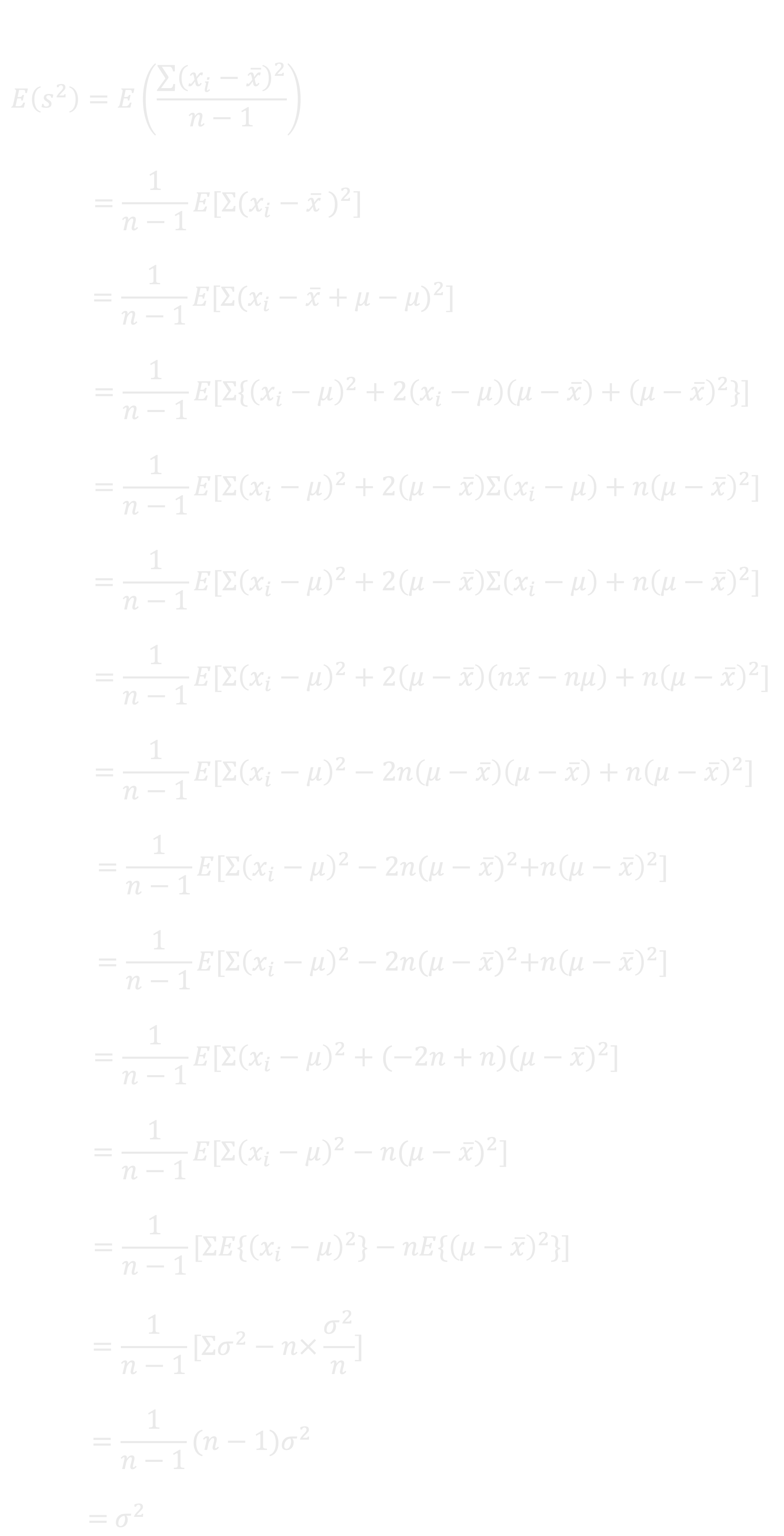
만약 n-1이 아닌 n으로 나눈다면 모분산이 (n-1)/n 만큼 작게 추정된다.
자유도
통계학에서 자유도(degrees of freedom, df) 는 통계적 추정을 할 때 표본자료 중 모집단에 대한 정보를 주는 독립적인 자료의 수를 말한다(출처: 위키피디아). 예를 들어 5개의 값으로 이루어진 표본에서 평균과 4개의 값을 알고있다면 마지막 5번째의 값이 무엇인지 알 수 있다. 또 다른 예시를 들어보면 10명의 사람이 아이스크림 10개 중 하나씩 골라서 먹는 상황에서 9명이 아이스크림을 고를 땐 본인이 먹고싶은 것을 자유롭게 선택할 수 있지만 마지막 10번째 사람은 남은 아이스크림 1개를 선택하게 된다.
표본편차, 표본분산을 구할 땐 표본평균에 따른다는 하나의 제약조건이 존재하기 때문에 n-1개의 표본만이 자유도를 가질 수 있다.
cf. 표본의 크기가 크다면 표본분산을 구할 때 n로 나누든 n-1로 나누든 큰 차이를 가지지 않는다.
참고문헌
- 위키피디아, 자유도
- 네이버 지식인, 표본분산 식에 대한 질문
- 티스토리 의미를 이해하는 통계학과 데이터 분석, 자유도(Degree of Freedom)에서 자유로워 지기
- 티스토리 귀퉁이 서재(Baek Kyun Shin), DATA - 7. 분산과 표준편차에서 n이 아니라 n-1로 나누는 이유 (자유도)
👩🏻💻개인 공부 기록용 블로그입니다
오류나 틀린 부분이 있을 경우 댓글 혹은 메일로 따끔하게 지적해주시면 감사하겠습니다.

댓글남기기